Why the Four-Phase Model is Becoming Obsolete

I don’t seem to be able to (coherently) fit this all into one piece so I’m going to try to do it as a short series. Many of these thoughts are loosely inspired by the work of Stuart Kauffman and Alicia Juarrero. If you haven’t already, check them both out. 

The four phase model of the game - attack, defensive transition, defense, attacking transition - has traditionally been treated as an “objective” property of the game. I’m going to argue that it has outlived its usefulness. As those staunch defenders of the truth will always tell you 2+2=4 no matter what you think about it. But have you ever noticed that it’s always framed as 2+2=4 vs 2+2=5 and never basic addition vs Reimannian geometry? The four-phase model holds true at the level of complexity it is able to deal with, but this level is no longer sufficient. 

The four-phase model tells us a team is always in one of four phases of a cycle. The team possesses the ball, loses it, defends, wins it back, attacks again, and so on. This seems hard to dispute. What other possible states (while the game is in play) might there be? We must ask, though, not how 2+2 might = 5, but rather if addition is a sufficient tool to deal with all phenomena. From the level of a single team, this is a powerful model, but I believe we are leaving single-team models behind in favor of two-team/system models. The perseverance of single-team models of the game is a testament to our deeply ingrained bias towards organismic asymmetry (the tendency to forget the ecosystems the organism is embedded within). One team can not play a sport. The actions of one team can not be understood without the opposition. Something about one hand clapping.

Once we start to think in two-team (henceforth “system”) terms, the shortcomings of the four-phase model become apparent. When the four phase model says a team is attacking, it is really saying that the system is in an attack-defend state.

When it says a team is in a defensive transition, it means that the system is in a defensive transition-attacking transition state. It always assumes symmetrical pairs of opposites. This seems reasonable given that most sports are zero-sum affairs.

Does one team always attack while the other defends, though? Let’s put it into an image and examine the possibilities.

Ignoring transitions (we’ll come back to those later) we have a 2x2 matrix with 4 cells. In the bottom-left and top right we see normal symmetrical opposites. I will refer to the line between these corners as the zero-sum axis (red arrows). Moving either direction along the zero-sum axis - towards A scoring in the bottom-left, and B scoring in the top-right - is the same thing, only mirrored. In the top-left and bottom-right corners, however, we have the attack-attack and defend-defend combinations. What can we say about this other diagonal axis (green arrow)? While attack-defend and defend-attack are mirror images of each other, attack-attack and defend-defend do not display this relationship. 

To say both teams are attacking is really to say that both teams have prioritised attacking, resulting in wild fluctuations between attack-defend and defend-attack - along the zero-sum axis, in other words. Both teams defending is an entirely different story, however. Nothing prevents both teams from defending simultaneously. True simultaneous attacking is excluded. Given this, let’s cut our matrix in half diagonally. It should now be easier to see that the defend-defend corner stabilizes the two-team system. We can stay in this stalemate as long as we want. Moving towards the attack-attack corner, however, the system tends towards collapse along the zero-sum axis.

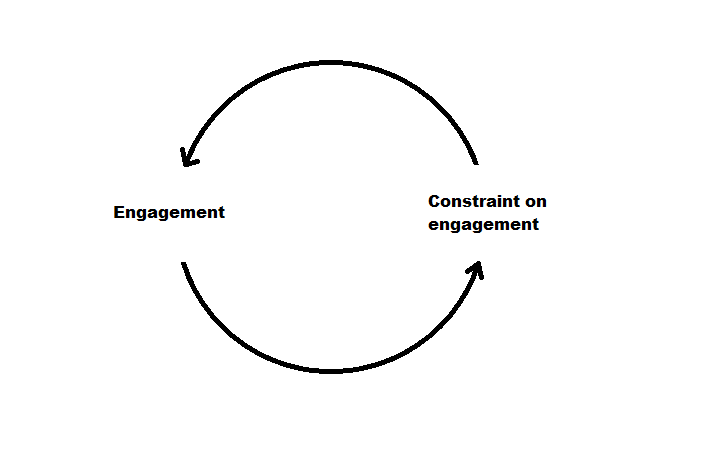
What should we make of the fact that both teams can defend simultaneously? That the game only moves along the zero-sum axis after it has moved up the engagement axis? We are saying that, if movement along the engagement axis necessarily precedes movement along the zero-sum axis we need to understand why the game leaves the bottom right corner (total disengagement) to begin with. The trouble is, nothing in the game explicitly prescribes this engagement. Here’s another way of thinking about it. Traffic signs tell you how you can and can’t drive, but they never tell you to drive in the first place. (Constraints-led approach works because sports are already just systems of constraints) 

Understanding the engagement axis always involves multiple levels of scale. Imagine a game in which the players seem quite disengaged and lethargic. This could be explained if we knew that one team scored five goals in the first half and both teams subsequently lost intensity. Let’s go up a level of scale. We see a game from kick-off this time, but both teams pass the ball around casually with zero attacking intent. We later find out that this was the final group game of a tournament in which both teams advanced with a draw. Again, we can only understand the engagement axis by moving to a higher level of scale. 

The fact that this seems so trivial is actually quite revealing. Consider the scenario in which you are with a group of friends and someone proposes a game no one has played before. It might be a great game, but it’s also quite possible that the group might stand around and not engage. A game or sport is only a set of constraints (rules) which people choose to engage with. The relationship is circular. Engagement is first constrained, but then (if people decide they like the game) also produced by the set of constraints known as that game. In other words, there are a set of rules known as football. Because these rules exist I decide to supply them with the engagement that makes them relevant, and a self-sustaining system is formed.

So we know that football has long since passed this test. We take for granted that our opposition will show up and engage with the game. We even anticipate various formations and tactics they may use. We would be wrong to confuse these later aspects of the game with “objective facts” of the game, though. They are only (currently) stable solutions or equilibrium points in the landscape. My claim is that to understand tactics more deeply we need to retrace the steps of our sport and understand our engagement with it. The most brilliant tactical advances are still only castles made of sand* - a perfect place to leave off before I get into what self-organized criticality and equilibrium points might have to do with the classic winning ugly vs losing pretty debate next time. 

*cringy reference to Bak’s landmark work on self-organized criticality using sandpiles

"When we try to pick out anything by itself, we find it hitched to everything else in the Universe." - John Muir